慶應NY学院の入試ではこのような問題が出題されます！

こんにちは、慶應義塾NY学院2020年度卒業生のRです。現在は慶應義塾大学に在学しており、ここでは自分がNY校で経験してきたことや情報をお伝えします。

今回はNY校の学院生活ではなく、キャタルで行っている入試対策を紹介します。2020年度以降NY校の入試問題は公表されていません、よって最新の過去問が手に入れられないのが現状です。キャタルでは、入試直後に生徒さん達にヒアリングし、入試傾向を聞き想定問題を作成しています。今回は、数学の問題を例に取り上げ解説していきます。

問題

定期テスト第12回より抜粋

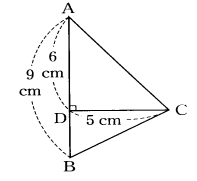
上の図形のように角Aと角Bがともに90°より小さい

角である三角形ABCにおいて、頂点Cから辺ABに

ひいた垂線と辺ABとの交点をDとする。

AB＝9cm,AD＝6cm,CD=5cmのとき、三角形ABCを、

ABCを軸として一回転させてできる立方体をAとする。

また円周率はπとする。この時、以下の問い(16),(17)に答えよ。

(16)立方体Aの表面積を求めよ。

(A) 45πcm2 　(B) 5(√61+√34)πcm2

(C) 80π cm3 　(D) 3(√51+√34)πcm2 　(E) 225πcm2

(17)立方体Aの体積を求めよ。

(A) 50cm3　 (B) 65cm3　 (C) 75cm3 　(D) 80cm3　 (E) 100cm3

解説

(16)立方体Aの表面積を求めよ。

立体Aは下の図のようになる。

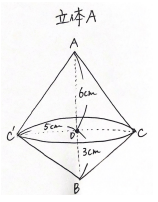
三平方の定理より、

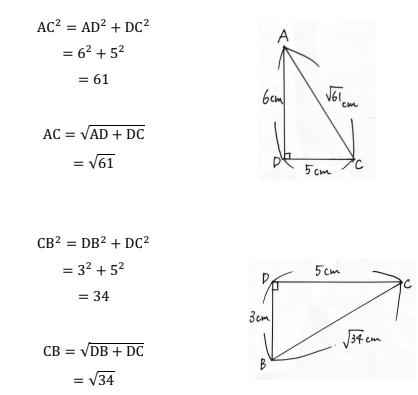
上の立体と下の立体に分けて、それぞれ展開図を描くと、以下のようになる。

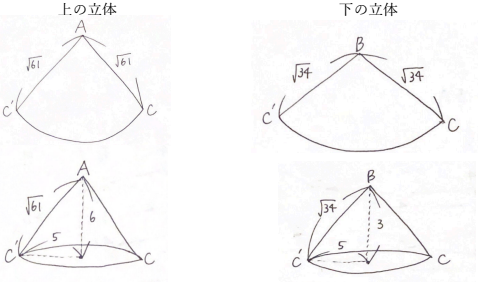
上の図の扇形の角度は、　底円の半径/母線　で求めることができるので、

立体Aの表面積は、

　　　　　　上の円錐の表面積(扇形の面積) +下の円錐の表面積(扇形の面積)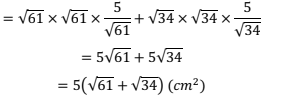

(17)立方体Aの体積を求めよ。

円錐の体積は、(底円の面積)x(高さ)x ⅓  によって求める事ができるので、

立体Aの体積は、

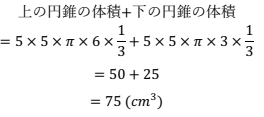
解く上でのポイント

表面積や体積を、三平方の定理や、基本的な公式などを組み合わせて求めるのが大切。　　　　　　　　　　　　　　　　　　　　　　ただ公式を覚えるだけはでなく、このような少し難易度の高い問題は応用をきかせて解きます。　　　　　　　　　　　　　　　　　　　　　　　　　難しい問題でもひとつひとつステップを踏んで解いていきましょう。

このような問題が出題されることが想定されます。キャタルの定期テストでは、同様の問題に取り組み対策しています。キャタルでは質の高い講師によって、NY学院の入試対策を行っています。

キャタルでは勉強以外にも色々な慶應NYの情報も教えています。一緒に勉強をして合格を目指しましょう！

↑①お子様のフルネーム ②お子様の生年月日 ③受験時期 ④英語の資格などお持ちであれば をこちらにお問い合わせください。担当者がご連絡いたします。